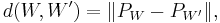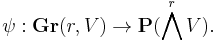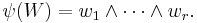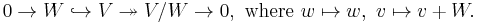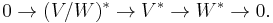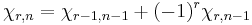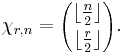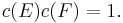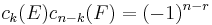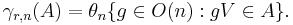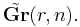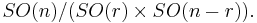Grassmannian

For other meanings, see Grassmannian (disambiguation).

In mathematics, a Grassmannian is a space which parameterizes all linear subspaces of a vector space V of a given dimension. For example, the Grassmannian Gr(1, V) is the space of lines through the origin in V, so it is the same as the projective space P(V). The Grassmanians are compact, topological manifolds.^[1] They are named in honor of Hermann Grassmann.

1 Motivation
- 1.1 History
2 Low dimensions
3 The Grassmannian as a set
4 The Grassmannian as a homogeneous space
5 The Grassmannian as a scheme
6 The Plücker embedding
7 The Grassmannian as a real affine algebraic variety
8 Duality
9 Schubert cells
- 9.1 Cohomology ring of the complex Grassmannian
10 Associated measure
11 Oriented Grassmannian
12 See also
13 References

Motivation

By giving a collection of subspaces of some vector space a topological structure, it is possible to talk about a continuous choice of subspace or open and closed collections of subspaces; by giving them the structure of a differential manifold one can talk about smooth choices of subspace. Though such concepts may seem strangely out of place they can coincide with things that one is interested in, and can describe ideas that could not be considered otherwise—or at least describe them more economically.

A natural example comes from tangent bundles of smooth manifolds embedded in Euclidean space. Suppose we have a manifold M of dimension r embedded in Rⁿ. At each point x in M, the tangent space to M can be considered as a subspace of the tangent space of Rⁿ, which is just R^r. The map assigning to x its tangent space defines a map from M to Gr(r, n). (In order to do this, we have to translate the geometrical tangent space to M so that it passes through the origin rather than x, and hence defines a r-dimensional vector subspace. This idea is very similar to the Gauss map for surfaces in a 3-dimensional space.)

This idea can with some effort be extended to all vector bundles over a manifold M, so that every vector bundle generates a continuous map from M to a suitably generalised Grassmannian—although various embedding theorems must be proved to show this. We then find that the properties of our vector bundles are related to the properties of the corresponding maps viewed as continuous maps. In particular we find that vector bundles with maps that are homotopic are isomorphic. But the definition of homotopic relies on a notion of continuity, and hence a topology.

History

The simplest Grassmannian that is not a projective space is Gr(2, 4). This was studied by Julius Plücker, as lines in projective 3-space, and he parameterized the space via Plücker coordinates. Hermann Grassmann generalized Plücker's work to general r-planes in n-space.

Low dimensions

When r = 2, the Grassmannian is the space of all planes through the origin. In Euclidean 3-space, a plane is completely characterized by the one and only line perpendicular to it (and vice-versa); hence Gr(2, 3) ≅ Gr(1, 3) ≅ P².

The Grassmannian as a set

Let V be a finite-dimensional vector space over a field k. The Grassmannian Gr(r, V) is the set of all r-dimensional linear subspaces of V. If V has dimension n, then the Grassmannian is also denoted Gr(r, n).

Vector subspaces of V are equivalent to linear subspaces of the projective space P(V), so it is equivalent to think of the Grassmannian as the set of all linear subspaces of P(V). When the Grassmannian is thought of this way, it is often written as Gr(r −1, P(V)) or Gr(r−1, n−1).

The Grassmannian as a homogeneous space

The quickest way of giving the Grassmannian a geometric structure is to express it as a homogeneous space. First, recall that the general linear group GL(V) acts transitively on the r-dimensional subspaces of V. Therefore, if H is a stabilizer of this action, we have

Gr(r, V) = GL(V)/H.

If the underlying field is R or C and GL(V) is considered as a Lie group, then this construction makes the Grassmannian into a smooth manifold. It also becomes possible to use other groups to make this construction. To do this, fix an inner product on V. Over R, one replaces GL(V) by the orthogonal group O(V), and by restricting to orthonormal frames, one gets the identity

Gr(r, n) = O(n)/(O(r) × O(n − r)).

In particular, the dimension of the Grassmannian is r(n−r);.

Over C, one replaces GL(V) by the unitary group U(V). This shows that the Grassmannian is compact. These constructions also make the Grassmannian into a metric space: For a subspace W of V, let P_W be the projection of V onto W. Then

$d(W, W') = \lVert P_W - P_{W'} \rVert,$

where $\lVert\cdot\rVert$ denotes the operator norm, is a metric on Gr(r, V). The exact inner product used does not matter, because a different inner product will give an equivalent norm on V, and so give an equivalent metric.

If the ground field k is arbitrary and GL(V) is considered as an algebraic group, then this construction shows that the Grassmannian is a non-singular algebraic variety. It can be shown that H is a parabolic subgroup, from which it follows that Gr(r, V) is complete. It follows by the Veronese embedding that the Grassmannian is a projective variety, and more easily it follows from the Plücker embedding.

The Grassmannian as a scheme

In the realm of algebraic geometry, the Grassmannian can be constructed as a scheme by expressing it as a representable functor.^[2]

The Plücker embedding

Main article: Plücker embedding

The Plücker embedding is a natural embedding of a Grassmannian into a projective space:

$\psi�: \mathbf{Gr}(r, V) \rightarrow \mathbf{P}(\bigwedge^r V).$

Suppose that W is an r-dimensional subspace of V. To define ψ(W), choose a basis w₁, ..., w_r of W, and let ψ(W) be the wedge product of these basis elements:

$\psi(W)=w_1 \wedge \cdots \wedge w_r.$

A different basis for W will give a different wedge product, but the two products will differ only by a non-zero scalar (the determinant of the change of basis matrix). Since the right-hand side takes values in a projective space, ψ is well-defined. To see that ψ is an embedding, notice that it is possible to recover W from ψ(W) as the set of all vectors w such that wΛψ(W) = 0.

The embedding of the Grassmannian satisfies some very simple quadratic polynomials called the Plücker relations. These show that the Grassmannian embeds as an algebraic subvariety of P(∧^rV) and give another method of constructing the Grassmannian. To state the Plücker relations, choose two r-dimensional subspaces W and Z of V with bases w₁, ..., w_r and z₁, ..., z_r, respectively. Then, for any integer k ≥ 0, the following equation is true in the homogeneous coordinate ring of P(∧^rV):

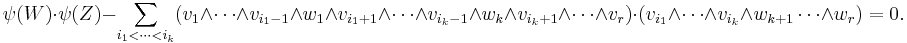
$\psi(W)\cdot\psi(Z) - \sum_{i_1 < \cdots < i_k} (v_1 \wedge \cdots \wedge v_{i_1 - 1} \wedge w_1 \wedge v_{i_1 %2B 1} \wedge \cdots \wedge v_{i_k - 1} \wedge w_k \wedge v_{i_k %2B 1} \wedge \cdots \wedge v_r)\cdot(v_{i_1} \wedge \cdots \wedge v_{i_k} \wedge w_{k%2B1} \cdots \wedge w_r) = 0.$

In the case that V has dimension 4, and r=2, the simplest Grassmannian which is not a projective space, the above reduces to a single equation. Denoting the coordinates of P(∧^rV) by 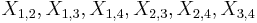$X_{1,2}, X_{1,3}, X_{1,4}, X_{2,3}, X_{2,4}, X_{3,4}$ , we have that Gr(2, V) is defined by the equation

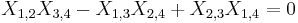$X_{1,2}X_{3,4} - X_{1,3}X_{2,4} %2B X_{2,3}X_{1,4} = 0$ .

In general, however, many more equations are needed to define the Plücker embedding of a Grassmannian in projective space.

The Grassmannian as a real affine algebraic variety

Let Gr(r, Rⁿ) denote the Grassmannian of r-dimensional subspaces of Rⁿ. Let M(n, R) denote the space of real n-by-n matrices. Consider the set of matrices A(r, n) ⊂ M(n, R) defined by X ∈ A (r, n) if and only if the three conditions are satisfied:

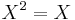$X^2 = X$ (ie: it is a projection operator)
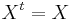$X^t = X$ (it is symmetric)
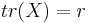$tr(X)=r$ (its trace is r)

A(r, n) and Gr(r, Rⁿ) are homeomorphic, with a correspondence established by sending X ∈ A(r, n) to the column space of X.

Duality

Every r-dimensional subspace W of V determines an (n – r)-dimensional quotient space V/W of V. This can be written down quickly as a short exact sequence:

$0 \to W \hookrightarrow V \twoheadrightarrow V/W \to 0, \ \text{where} \ w \mapsto w, \ v \mapsto v %2B W.$

Taking the dual to each of these three spaces and linear transformations yields an inclusion of (V/W)* in V* with quotient W*:

$0 \to (V/W)^* \to V^* \to W^* \to 0.$

Using the natural isomorphism of a finite-dimensional vector space with its double dual shows that taking the dual again recovers the original short exact sequence. Consequently there is a one-to-one correspondence between r-dimensional subspaces of V and n−r-dimensional subspaces of V*. In terms of the Grassmannian, this is a canonical isomorphism

Gr(r, V) ≅ Gr(n − r, V*).

Choosing an isomorphism of V with V* therefore determines a (non-canonical) isomorphism of Gr(r, V) and Gr(n − r, V). An isomorphism of V with V* is equivalent to a choice of an inner product, and with respect to the chosen inner product, this isomorphism of Grassmannians sends an r-dimensional subspace into its (n – r)-dimensional orthogonal complement.

Schubert cells

The detailed study of the Grassmannians uses a decomposition into subsets called Schubert cells, which were first applied in enumerative geometry. The Schubert cells for Gr(r, n) are defined in terms of an auxiliary flag: take subspaces V₁, V₂, ..., V_r, with V_i contained in V_{i + 1}. Then we consider the corresponding subset of Gr(r, n), consisting of the W having intersection with V_i of dimension at least i, for i = 1 to r. The manipulation of Schubert cells is Schubert calculus.

Here is an example of the technique. Consider the problem of determining the Euler characteristic of the Grassmannian of r-dimensional subspaces of Rⁿ. Fix a one-dimensional subspace R ⊂ Rⁿ and consider the partition of Gr(r, n) into those r-dimensional subspaces of Rⁿ that contain R and those that do not. The former is Gr(r − 1, n − 1) and the latter is a r-dimensional vector bundle over Gr(r, n − 1). This gives recursive formulas:

$\chi_{r,n} = \chi_{r-1,n-1} %2B (-1)^r \chi_{r, n-1}\,$

where by design 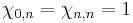$\chi_{0,n} = \chi_{n,n} = 1$ . If one solves this recurrence relation, you have the formula: 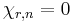$\chi_{r,n} = 0$ if and only if n is even and r is odd. Otherwise:

$\chi_{r, n} = {\lfloor \frac{n}{2} \rfloor \choose \lfloor \frac{r}{2} \rfloor }.$

Cohomology ring of the complex Grassmannian

Every point in the complex Grassmannian manifold Gr(r, n) defines an r-plane in n-space. Fibering these planes over the Grassmannian one arrives at the vector bundle E which generalizes the tautological bundle of a projective space. Similarly the (n − r)-dimensional orthogonal complements of these planes yield an orthogonal vector bundle F. The integral cohomology of the Grassmannians is generated, as a ring, by the Chern classes of E. In particular, all of the integral cohomology is at even degree as in the case of a projective space.

These generators are subject to a set of relations, which defines the ring. The relations merely state that the direct sum of the bundles E and F is trivial. Functoriality of the total Chern classes allows one to write this relation as

$c(E)c(F)=1.$

The quantum cohomology ring was calculated by Edward Witten in The Verlinde Algebra And The Cohomology Of The Grassmannian. The generators are identical to those of the classical cohomology ring, but the top relation is changed to

$c_k(E)c_{n-k}(F)=(-1)^{n-r}$

reflecting the existence in the corresponding quantum field theory of an instanton with 2n fermionic zero-modes which violates the degree of the cohomology corresponding to a state by 2n units.

Associated measure

When V is n-dimensional Euclidean space, one may define a uniform measure on Gr(r, n) in the following way. Let θ_n be the unit Haar measure on the orthogonal group O(n) and fix V in Gr(r, n). Then for a set A ⊆ Gr(r, n), define

$\gamma_{r, n}(A)=\theta_{n}\{g\in O(n):gV\in A\}.$

This measure is invariant under actions from the group O(n), that is, γ_{r, n} (g A) = γ_{r, n} (A) for all g in O(n). Since θ_n (O(n))=1, we have γ_{r, n} (Gr(r, n))=1. Moreover, γ_{r, n} is a Radon measure with respect to the metric space topology and is uniform in the sense that every ball of the same radius (with respect to this metric) is of the same measure.

Oriented Grassmannian

This is the manifold consisting of all oriented r-dimensional subspaces of Rⁿ. It is a double cover of Gr(r, n) and is denoted by:

$\tilde{\mathbf{Gr}}(r, n).$

As a homogeneous space can be expressed as:

$SO(n)/(SO(r)\times SO(n-r)).$

References

^ Milnor, J. W.; Stasheff, J. D. (1974). Characteristic Classes. Princeton University Press. pp. 57–59. ISBN 0691081220.
^ Grothendieck, Alexander (1971). Éléments de géométrie algébrique. 1 (2nd ed.). Berlin, New York: Springer-Verlag. ISBN 978-3-540-05113-8 , Chapter I.9
^ Morel, Fabien; Voevodsky, Vladimir (1999). "A^1-homotopy theory of schemes". Publications Mathématiques de l'IHÉS (90): 45–143. ISSN 1618-1913. MR 1813224. http://archive.numdam.org/article/PMIHES_1999__90__45_0.pdf. Retrieved 09/05/2008 , see section 4.3., pp. 137–140

Hatcher, Allen (2003). Vector Bundles & K-Theory (2.0 ed.). http://www.math.cornell.edu/~hatcher/VBKT/VBpage.html. section 1.2
Milnor, John W.; Stasheff, James D. (1974). Characteristic classes. Annals of Mathematics Studies, No. 76. Princeton University Press, Princeton, NJ; University of Tokyo Press, Tokyo. ISBN 0-691-08122-0. see chapters 5-7
Joe Harris, Algebraic Geometry, A First Course, (1992) Springer, New York, ISBN 0-387-97716-3
Pertti Mattila, Geometry of Sets and Measures in Euclidean Spaces, (1995) Cambridge University Press, New York, ISBN 0-521-65595-1